前言 :
以下內容皆使用Weka 3.8.2去做演算法的分析,並且文章會根據分群分析、分類分析,按照這個排序分成兩大部分做探討。
兩個部分皆採用兩種不同類型的Datasets ,「現有Dataset」與「創意Dataset」;此外,每一個Dataset都會用兩種屬於該分群分析或分類分析的演算法。
分群分析會使用的演算法為① K-Means(K-平均法)與② Expectation Maximization, EM(期望最大化法);分類分析會使用的演算法為① Decision Tree(決策樹)與② REPTree(快速決策樹)。
一、 Clustering Analysis(分群分析) :
- 現有Dataset — User Knowledge Modeling Data Set
User Knowledge Modeling Data Set 來源 → https://archive.ics.uci.edu/ml/datasets/User+Knowledge+Modeling
User Knowledge Modeling Data Set是去調查受試者本身知識的掌握程度,資料筆數包含了258筆受試者的資料,欄位屬性有「STG(The degree of study time for goal object materials)(研讀目標科目所花費時間之程度)」、「SCG(The degree of repetition number of user for goal object materials)(重複溫習目標科目之程度)」、「STR(The degree of study time of user for related objects)(研讀相關科目所花費時間之程度)」、「LPR(The exam performance of user for related objects with goal object)(相關科目的考試表現)」、「PEG(The exam performance of user for goal objects)(目標科目的考試表現)」、及「UNS(The knowledge level of user)(受試者的知識水平)」,共上述六種屬性。
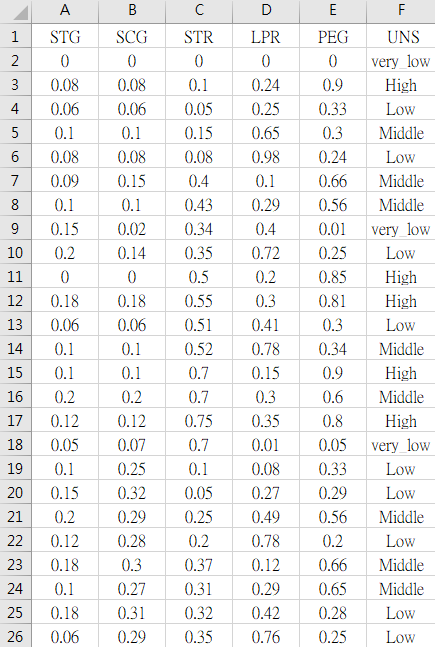
258筆資料中,每個欄位皆為從0到1之間的數值,越接近1代表該受試者在該屬性欄位的表現越好,反之亦然。
「UNS(受試者的知識水平)」的欄位屬性,表現由好到壞包含了「High」、「Middle」、「Low」、及「very_low」。
本次實作將使用K-Means(K-平均法)與Expectation Maximization, EM(期望最大化法)這兩種演算法來做分析,並會針對兩者求得之分群結果,判斷其分群之依據,以及相同分群內的相似性、不同分群間的差異性。
① K-Means(K-平均法)
根據參考網址(https://docs.microsoft.com/zh-tw/sql/analysis-services/data-mining/microsoft-clustering-algorithm-technical-reference)的說明 :
K-Means是將群集當中項目之間的差異最小化,並將群集之間的距離最大化。 K-means 中的「means」是指群集的「距心」,這是任意選擇的資料點,在選擇後會反覆調整,直到能代表群集中所有資料點的真正平均值為止。「k」則是指用來植入群集程序的任意數目的資料點。
K-means 演算法會計算群集中資料記錄之間的歐氏距離平方(Squared Euclidean Distance)以及代表群集平均值的向量,然後在總和達到最小值時聚合於最終的一組 K 群集。此外,K-Means會將每個資料點剛好指派給一個群集,而不允許成員資格有任何不確定性,且群集中的成員資格會以和距心的距離來表示。
於前面有提到,此筆現有Dataset被「UNS(受試者的知識水平)」區分為了四群,故在一開始設定K-Means的參數時,將「numClusters」設為4(預設為2)。
此外,「 classes to clusters evaluation」這個選項可以用來檢驗最後得到的分群結果,與我們選給「 classes to clusters evaluation」的欄位屬性,兩者之間的關聯性是強或弱。這個步驟可以在最後評估階段的時候,得知何種欄位屬性與我們的分群結果有較強的相關性。
因我們想了解「UNS(受試者的知識水平)」與分群結果之間的相關性為何,因此會把「 classes to clusters evaluation」設定為「(Nom)UNS」。
使用K-Means所得到的分析結果如下圖:
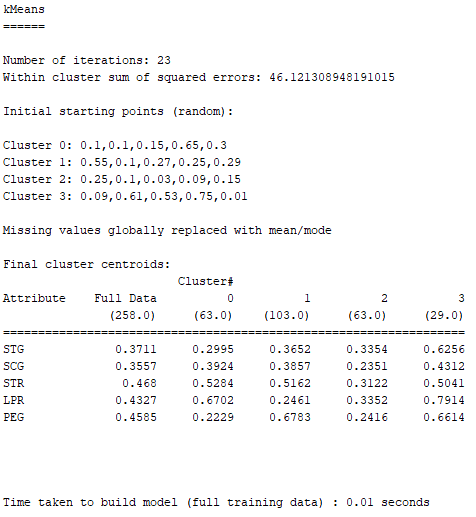
根據上圖, 每個數值表該Cluster對該欄位屬性的平均值,越靠近0代表該Cluster越多人沒有這個欄位屬性的特色;越靠近1表示越多人有這個欄位屬性的特色。
Cluster 3 :
此分群的共同點在於每個欄位的屬性幾乎都表現得很優異,尤其是在LPR(相關科目的考試表現)」、PEG(目標科目的考試表現)的成績都屬於前段班;此外,在STR(研讀相關科目所花費時間之程度)即使輸給Cluster 0,但LPR的表現卻依然拿了第一名,代表Cluster 3的人不用花太多時間在讀相關科目,考試的時候一樣能拿到比其他分群的人還高的分數。故Cluster 3的UNS(受試者的知識水平)可以被判定為High。
Cluster 0與Cluster 2 :
兩個分群的人在各個欄位屬性的表現都非常低迷,除了Cluster 0的相關科目成績表現還可以(但也是因為他們花在研讀相關科目的時間很多),總的來說,兩個分群的人花在研讀目標科目或相關科目的時間都很少、也不愛重複溫習、然後兩類科目的考試成績也不是特別優異。因此,這兩群的UNS(受試者的知識水平)有極大的可能是Low與very_low。
但兩個分群當中,誰是Low、誰又是very_low呢? 關鍵的欄位屬性是SCG(重複溫習目標科目之程度)與PEG(目標科目的考試表現),Cluster 0的SCG明明比Cluster 2高出很多,還比Full Data的平均值還高,代表Cluster 0的人花費很多時間在重複溫習目標科目,結果……最後考出來的目標科目分數,還比Cluster 2的人低,實在是很悲慘。
因此,UNS(受試者的知識水平)的選擇上,我們判定Cluster 0為very_low、Cluster 2為Low。
Cluster 1 :
整體表現明顯的可以看出很平庸,不好也不壞,壞的部分是STR(研讀其他相關科目所花費時間之程度)與LPR(其他相關科目的考試表現),花費的時間算多,可是相關科目考出來的分數卻是全部分群裡的最低分;好的部分是STG(研讀目標科目所花費時間之程度)、SCG(重複溫習目標科目之程度)、與PEG(目標科目的考試表現),花在研讀跟重複溫習目標科目的時間算是不多也不少,可是目標科目考出來的分數居然是全部分群裡的最高。
總結上述,我們可以將Cluster 1的UNS(受試者的知識水平)判定為Middle。
用上面四個分群推斷的結果,來與下面K-Means用classes to clusters evaluation跑出的結果來做比對,發現兩者的答案完全吻合 :

但上圖中的Incorrectly clustered instances(不正確的群集案例)約為40.7%,故其還不能算是個非常準確的模型,慶幸的是尚未超過50%。
倘若未來遭遇正確性非常非常低的模型,在這種情況下,該模型將無法告訴我們任何資訊,也無法讓我們拿這個模型去預測未知的資料,因為它的資訊參考價值不高,假如我們依然執意選擇採納這個模型帶給我們的資訊,可能就會導致決策者擬定出錯誤的政策或決定,導致浪費時間、金錢……等成本。
會取得這樣糟糕的模型結果,可能的原因有兩種。第一,這份創意Dataset的資料組成本身就有問題,可能兩種現有Datasets的相關性原本就不高,使得演算法無法成功從中將資料完美分群;第二,或許我們在這裡選擇用K-Means、EM,亦或者是全部分群分析的方法,本身就是一個錯誤的決定。因此若要持續分析這筆創意Dataset,可能就要多方嘗試其他演算法,畢竟要為數據選擇適合的模型,最後的結果才能讓我們挖掘出有意義的資訊。
② Expectation Maximization, EM(期望最大化法)
根據參考網址(https://docs.microsoft.com/zh-tw/sql/analysis-services/data-mining/microsoft-clustering-algorithm-technical-reference)的說明 :
EM是使用高斯分配(Gaussian Distribution),也就是用常態分配來描述該案例隸屬於某群集的機率密度,利用此機率函數來取代剛性群集的距離函數。
在 EM 群集中,演算法會反覆地精簡初始群集模型以符合資料,並判斷資料點存在於群集內的機率,演算法會在機率模型符合資料時結束此程序。
如果在處理程序的期間產生空白的群集,或如果一或多個群集的成員資格落在指定臨界值之下,則具有低母體的群集會在新的資料點重設種子,然後再重新執行 EM 演算法。
而在前面介紹K-Means的部分有提到,K-Means會將每個資料點剛好指派給一個群集,而不允許成員資格有任何不確定性,且群集中的成員資格會以和距心的距離來表示;然而,EM 群集方法的結果並非機率式,這代表每個資料點都屬於所有的群集,但每次指定資料點給群集時都具有不同的機率。 因為此方法允許群集重疊,所以所有群集中的項目總和可能會超過定型集中的項目總數。
在Weka 3.8.2選擇使用EM這個演算法的時候,設定參數的部分與K-Means一樣,「numClusters」設定為4,而一開始的預設值為-1,其意思代表的是讓EM自己決定要分幾群;此外,我們一樣將「 classes to clusters evaluation」設定為「(Nom)UNS」。
下面就是利用EM分析現有Dataset所求得的結果 :
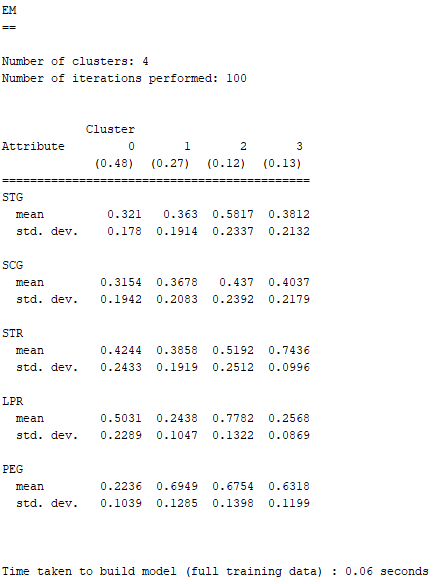
EM的表達方式與K-Means略為不同,若EM的欄位屬性屬於名目資料,則欄位屬性當中的每個選項,都會有一個數值與其呼應,該數值代表的即是那個選項發生的機率;若屬於數值資料,則會顯示其平均數與標準差。
因為STG、SCG、STR、LPR、與PEG皆為數值型資料,故EM顯示了它們的平均數與標準差。
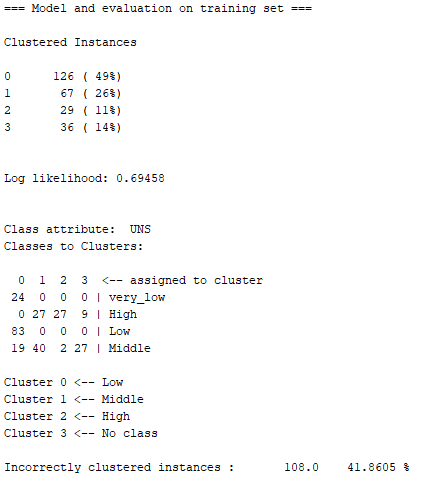
由上面兩張圖可以得知,EM分析現有Dataset的分群結果,與K-Means的有點類似。唯一不同的地方在於,以分成四群的方式將結果分析出來之後,EM似乎認為Cluster 3與very_low之間沒有這麼大的相關性,而最後得到的Incorrectly clustered instances(不正確的群集案例)也比K-Means略高了一點,約為41.86%。
那如果我們讓EM一開始就自己決定分群數呢? 也就是將「numClusters」還原為EM預設的-1
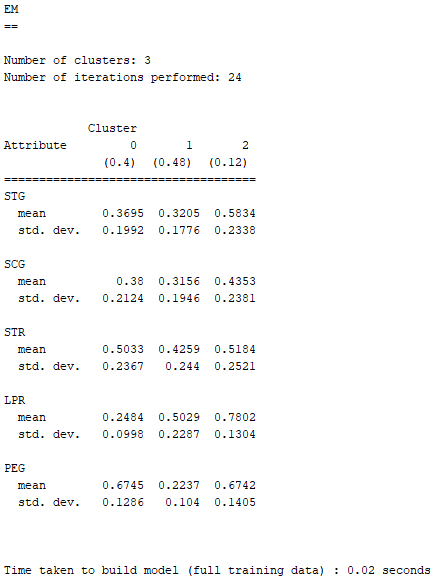
由EM自己決定分群數量的結果,它將現有Dataset分成了三群,這個結果變得非常好解釋 :
Cluster 2在LPR(其他相關科目的考試表現)與PEG(目標科目的考試表現)都有非常亮眼的表現,可以馬上判定UNS(受試者的知識水平)為High。
Cluster 1與Cluster 0之間處於互相消長的狀態,兩者數據的好壞程度很接近。Cluster 1在PEG(目標科目的考試表現)是三個分群中表現最差;Cluster 0在LPR(其他相關科目的考試表現)是三個分群中表現最差。
然而,Cluster 1的LPR(其他相關科目的考試表現)不是三個分群中表現最好的,但Cluster 0的PEG(目標科目的考試表現)卻是超越Cluster 3拿到三個分群中的第一名。
因此在UNS(受試者的知識水平)的選擇上,可以將Cluster 1判定為Low、Cluster 0判定為Middle。
令人開心的消息是,交給EM自己決定分群數量,並將「 classes to clusters evaluation」設定為「(Nom)UNS」之後,求得的Incorrectly clustered instances(不正確的群集案例)下降到了約31.4%。
或許是因為少了very_low這個原本很難去跟分群找出相關性的欄位屬性,因此現在分成三群之後,EM就能更完美地把三個分群對應到High、Middle、Low。
2. 創意Dataset
小時候常聽大人說,左撇子的人會比右撇子的人聰明,對於左撇子是否會影響大腦,上網查了一下也發現學界至今仍然對這個問題爭論不休。
受到這個問題的發想,於是在創意Dataset的部分,我們假設還有調查258位受試者的慣用手為何 :
其中,「Hand(慣用手)」包含了left與right。
因此我們可以去分析,在這個純屬虛構的創意Dataset,裡面的左撇子在知識水平以及平常考試的表現上是否有比右撇子還要優異?
下面一樣使用K-Means(K-平均法)與 Expectation Maximization, EM(期望最大化法)這兩種方法來依序分析這筆虛構的創意Dataset :
① K-Means(K-平均法)
在一開始設定參數的部分,因為希望K-Means會以「Hand(慣用手)」裡面的左手跟右手去做分群,故先將「numClusters」設為原本就是預設值的2。
然而,在這邊「classes to clusters evaluation」就不做設定了,因為我們單純想知道K-Means分群之後的結果,是不是有用「Hand(慣用手)」這個欄位屬性去做分群,故在這邊選擇「Use training set」。
下圖就是K-Means分析完之後的結果 :
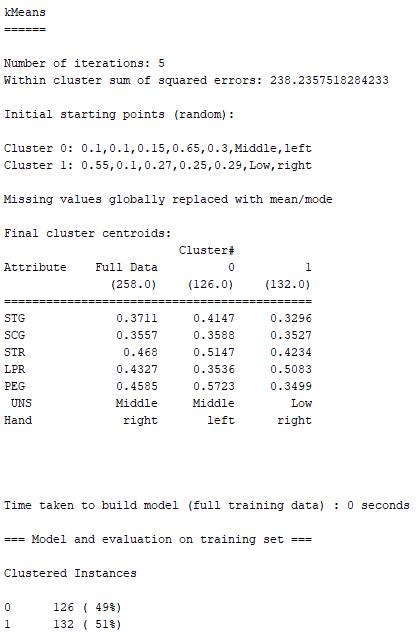
根據上圖,「Hand(慣用手)」為left、且「UNS(受試者的知識水平)」為Middle的人被歸類在Cluster 0;「Hand(慣用手)」為right、且「UNS(受試者的知識水平)」為Low的人被歸類在Cluster 1。
我們再接續看看EM的分析是否會和K-Means告訴我們的結果一樣,並會在最後一起做出結論。
② Expectation Maximization, EM(期望最大化法)
一開始在Weka 3.8.2設定EM參數時,如同前面一樣,要先將「numClusters」設定為2。
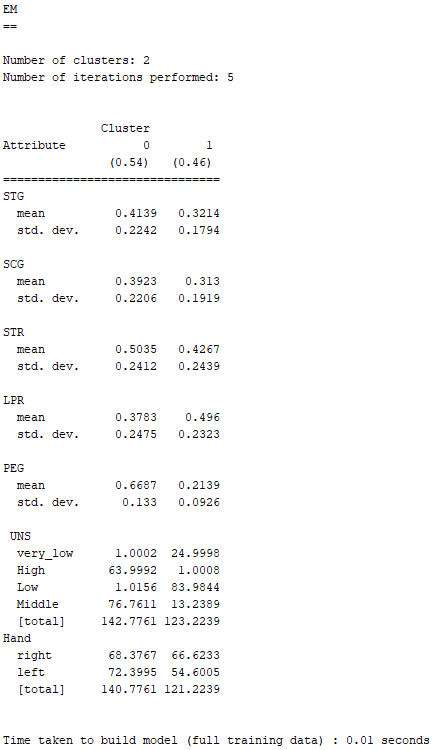
根據上圖由EM分析出來的結果,可以發現其與K-Means的結果吻合。Cluster 0皆被劃分為左撇子的人,且知識水平為Middle;Cluster 1皆被劃分為右撇子的人,且知識水平為Low。
因此,在這筆虛構創意Dataset的情境之下,K-Means與EM這兩種演算法皆分析出左撇子的知識水平會較右撇子的知識水平高,
不過左、右撇子的知識水平差距也不會到太大,因為左撇子在UNS(受試者的知識水平)只被判定為Middle,而沒有到High;右撇子也只在UNS被判為Low,而不是very_low。
此外,左、右撇子在所有欄位屬性當中,差距最明顯的也只發生在PEG(目標科目的考試表現),兩者最大的差異就發生在這個欄位屬性。
二、 Classification Analysis(分類分析) :
- 現有Dataset — bank-data.csv
bank-data.csv 來源 → https://learnersdesk.weebly.com/weka-tutorials.html
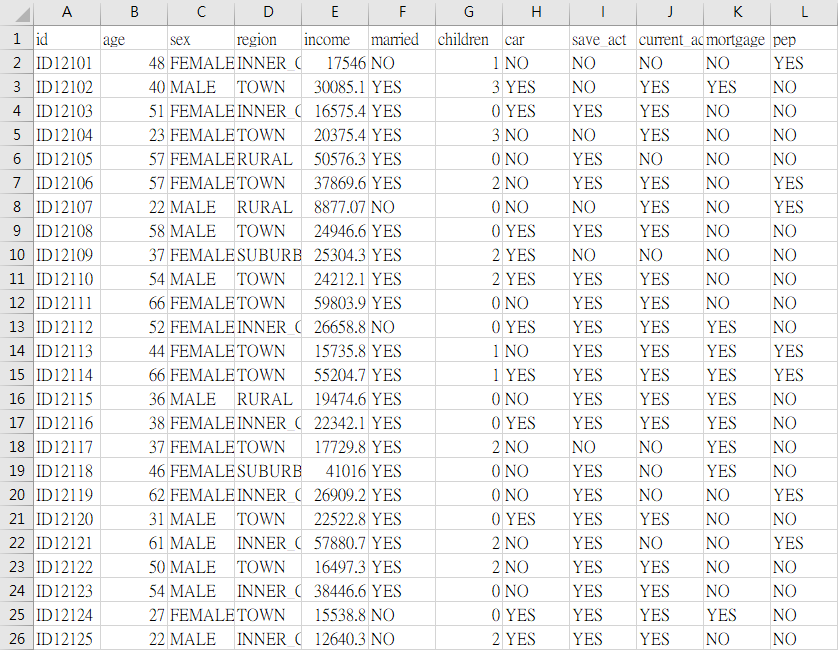
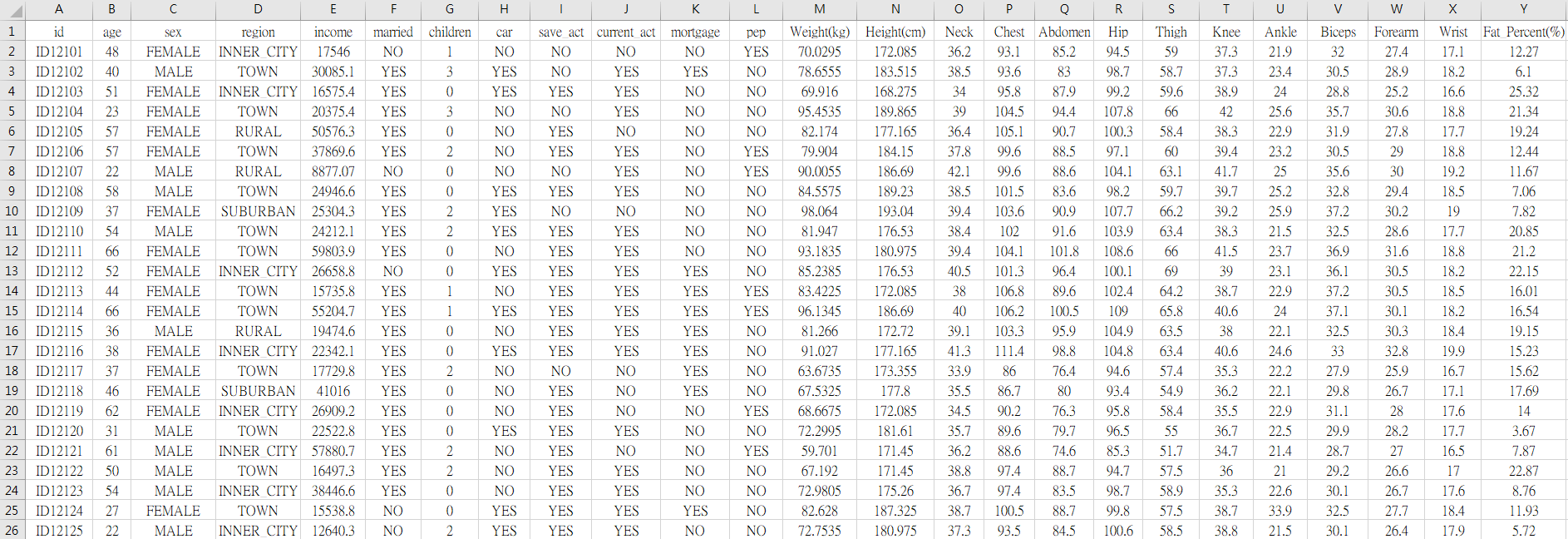
bank-data包含了某銀行600位客戶的個人資料,其欄位屬性總共有12種,分別為「id(客戶編號)」、「age(年齡)」、「sex(性別)」、「region(居住地區)」、「income(收入)」、「married(是否已婚)」、「children(有幾位小孩)」、「car(是否有車)」、「save_act(是否有儲蓄帳戶)」「current_act(是否有經常帳戶)」、「mortgage(是否有抵押借款的紀錄)」,以及「pep(是否有個人持股計畫)」。
其中,「region(居住地區)」包含了四種選項,「INNER_CITY(內城區、貧民窟) 」、「TOWN(都會區、市中心)」、「RURAL(農村、鄉村)」、「SUBURBAN(郊區)」;「children(有幾位小孩)」最少有0位,最多則有3位。
而在這12種欄位屬性中,「pep(是否有個人持股計畫)」讓我最感興趣,pep的全稱為 personal equity plan
而根據MBA智庫百科在其網站中提到(http://wiki.mbalib.com/zh-tw/%E4%B8%AA%E4%BA%BA%E6%8C%81%E8%82%A1%E8%AE%A1%E5%88%92) :
「 個人持股計劃(Personal equity plan),是英國政府於西元1987年向普通投資者推行的擁有公司股份和進行行業投資的計劃。這份投資能享受所得稅免除的優惠。直到西元1999年,個人持股計劃最終被個人存款賬戶(Individual saving account)取代。」。
因此,我想要了解這份bank-data當中的600位民眾,在當時西元1987年至1999年辦理pep的情況為何?以及何種屬性對於「判斷該名客戶是否是pep」的影響力較顯著?
以下我將分別利用Decision Tree(決策樹)與REPTree(快速決策樹)這兩種方法來分析bank-data這筆資料。
首先,第一個欄位屬性「id(客戶編號)」針對我欲分析的問題暫無參考價值,故在挑選屬性的步驟時,我選擇將其刪除。此外,由於我想得知何種屬性對於「判斷該名客戶是否有pep」的影響力較顯著,故接下來我將「pep(是否有個人持股計畫)」這個欄位屬性設為訓練決策樹的依據,待上述步驟完成之後,下面就是由Weka 3.8.2跑出的分析內容與視覺化的結果 :
① Decision Tree(決策樹)
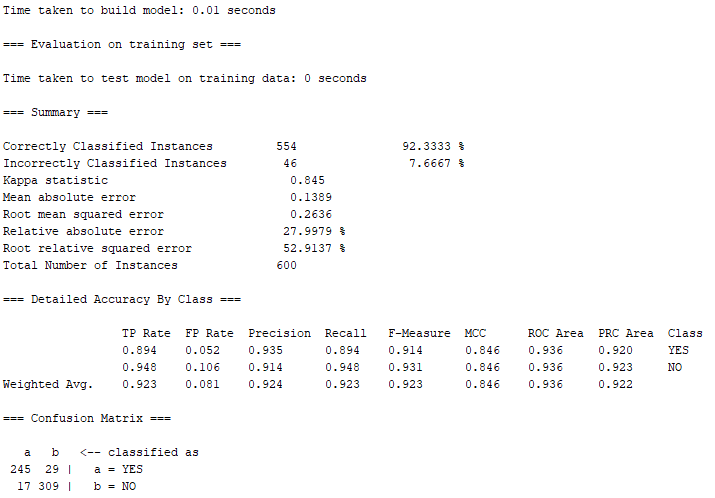
由上圖可知,600筆訓練出來的資料當中,有554筆屬於Correctly Classified Instances(正確的分類案例),正確率高達約92.33%;另外僅有46筆屬於Incorrectly classified instances(不正確的分類案例),錯誤率只有約7.67%。
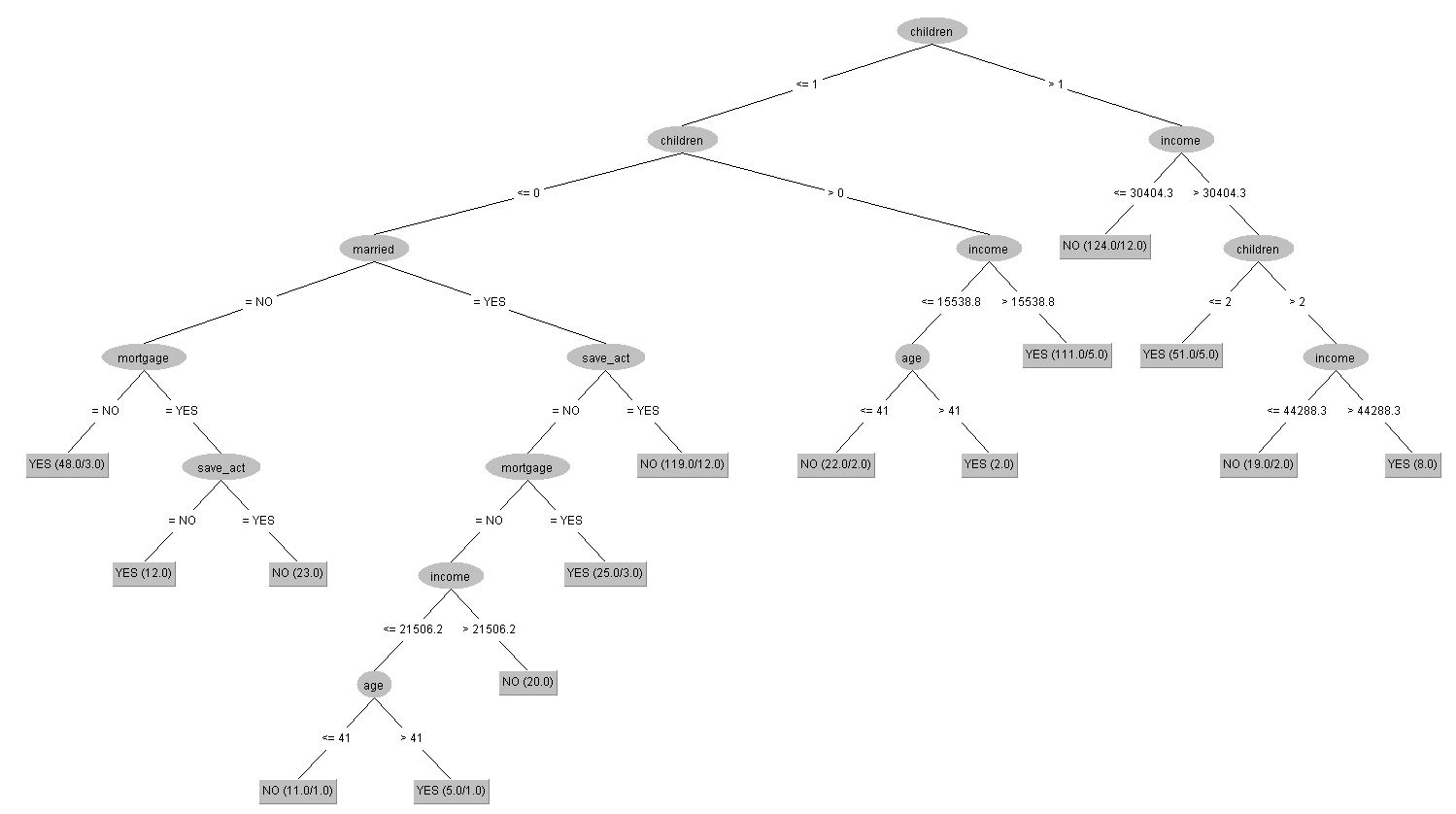
上圖是視覺化過後的決策樹之結果,總共有八種情況是被決策樹視為容易出現有pep的情形,其中,有四種情況能很直觀的去推斷這些類型的客戶有很高的機率會辦理pep,更有三種是僅考量了收入與小孩數量的屬性 : a. 當有客戶是有3位小孩、且收入大於44288.3元;b. 有2位小孩、且收入大於30404.3元;c. 有1位小孩、且收入大於15538.8元;d. 沒有小孩、且沒有結婚、且沒有抵押借貸紀錄。除此之外,「children(有幾位小孩)」被定義為判斷客戶是否為pep的最初屬性,再往下一層的屬性則多了「income(收入)」,換句話說,這兩項屬性可以被視為是資料當中比較重要的分類依據。
② REPTree(快速決策樹)
REPTree在Weka 3.8.2的說明內容如下:「Fast decision tree learner. Builds a decision/regression tree using information gain/variance and prunes it using reduced-error pruning(with backfitting). Only sorts values for numeric attributes once. Missing values are dealt with by splitting the corresponding instances into pieces(i.e. as in C4.5).」。
參考此連結(http://www.voidcn.com/article/p-gcpdepka-bbe.html)的網站對於REPTree與Decision Tree的比較之後,下方統整出幾個REPTree的主要特色以及其與Decision Tree的差異 :
在節點選擇的方式上,REPTree採用的是information gain(信息增益);Decision Tree則是information gain rate(信息增益率)。此外,REPTree會用varience(方差)來判斷 values for numeric attributes(數值型的屬性)是否已經結束分裂。
而與Decision Tree相比,REPTree在處理資料的過程中多了一道backfit的程序,backfit會改變已有的tree節點以及其子節點的class分佈,且class分佈將直接被用於實例的預測。Decision Tree會沒有backfit的原因是,Decision Tree已有自己獨立的classify instance,過程不依賴資料集的分佈;而REPTree的classify instance是調用基類的過程,會需要自己存儲一個分佈,進而透過傳入一個新的資料集以用backfit來防止過度擬合。
此外,在處理values for numeric attributes的時候,Decision Tree對資料集內的每個subset(子集)都要進行排序;而REPTree會直接在主流層中對所有屬性只進行一次排序,並生成index傳給tree節點來進行處理。 因此,Decision Tree所耗的時間比較長,而REPTree則是會佔用較大的內存。
下面就是利用Weka 3.8.2當中,以REPTree的方法所跑出的分析內容與視覺化的結果 :
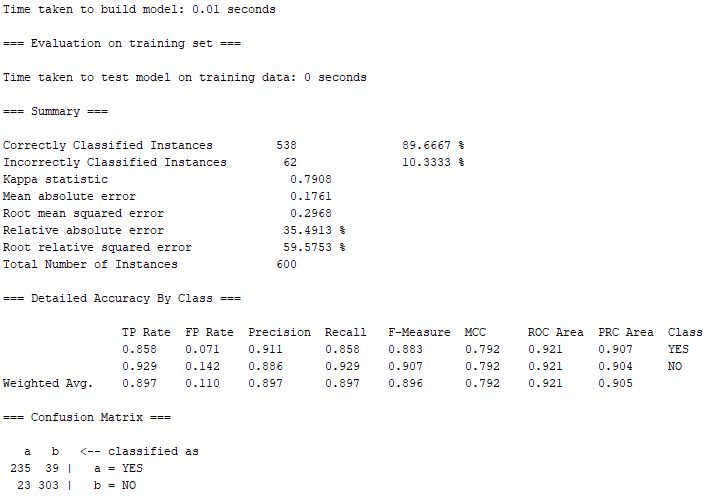
根據上圖的結果,有538筆屬於Correctly Classified Instances(正確的分類案例),正確率約89.67%;另外有62筆屬於Incorrectly classified instances(不正確的分類案例),錯誤率約10.33%。相較於① Decision Tree(決策樹),REPTree(快速決策樹)的正確率仍略低於以Decision Tree所跑出來的結果。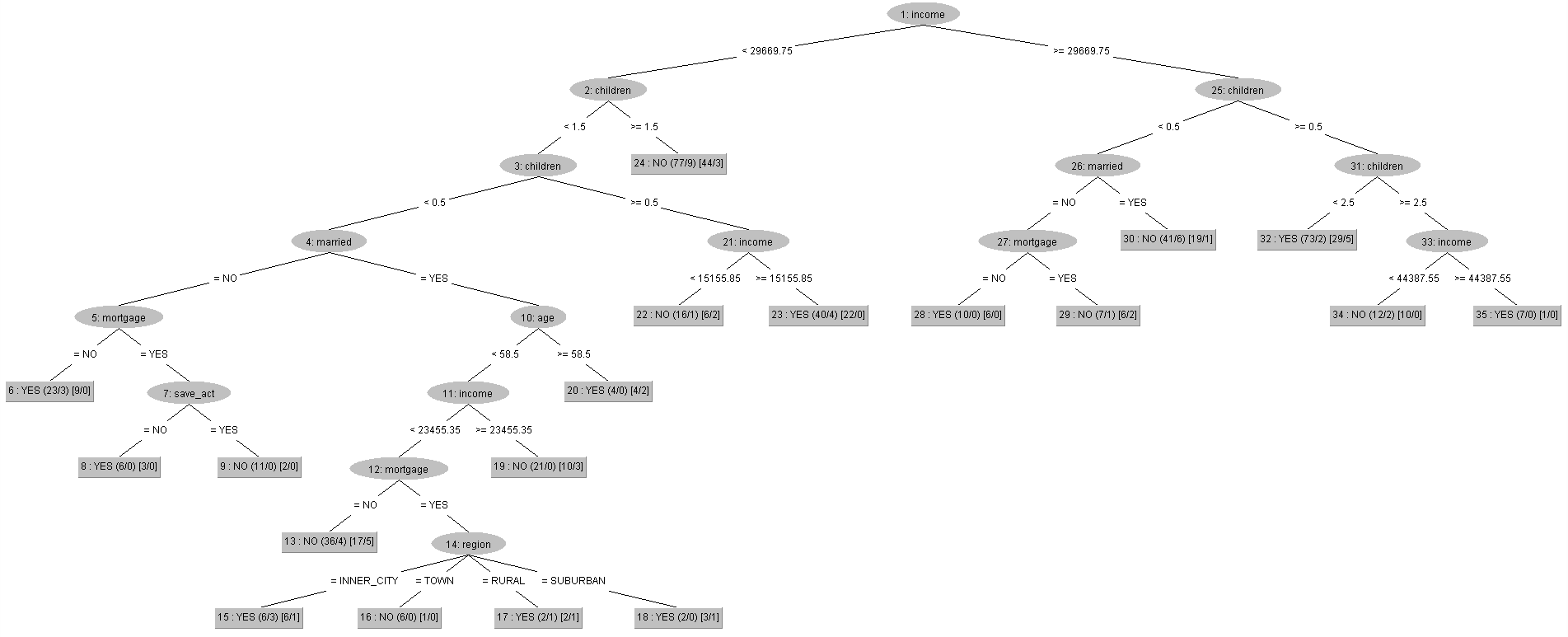
上面視覺化之後的結果與① Decision Tree(決策樹)的結果相比,② REPTree(快速決策樹)是以「income(收入)」作為其判斷客戶是否辦理pep的最初屬性,「children(有幾位小孩)」則被移到了第二層,但income、children這兩種屬性都被兩種方法共同視為所有屬性中,比較重要的分類依據。
其中,REPTree則有十種情況是被決策樹視為容易出現有pep的情形,下面5種情況則是較直觀能判斷出是否有很大機率會辦理pep的情形 : a. 當有客戶是收入大於等於44387.55元、且有3位小孩;b. 收入大於等於29669.75元、且有1位或2位小孩;c. 收入大於等於29669.75元、且沒有小孩、且沒有結婚、且沒有抵押借貸紀錄;d. 收入大於等於15155.85、且有1位小孩;e. 收入小於29669.75元、且沒有小孩、且沒有結婚、且沒有抵押借貸紀錄。而c.與e.可以融合成為「沒有小孩、且沒有結婚、且沒有抵押借貸紀錄」的客戶。
總而言之,REPTree定義出會辦理pep的情況雖然較Decision Tree多出了兩種,但其實兩者最後歸納出的屬性條件非常相近。而REPTree的正確率會比Decision Tree略低的原因,可能在於Decision Tree對資料集內的每個subset(子集)都會進行排序,這樣當然比較花時間,因為是一個一個子集慢慢去做分析,不過展示出來的結果正確度可能就因此會比較高;而REPTree在處理速度上雖然較快,但正確度就稍微低於Decision Tree。
透過上述兩種分類分析方法所求得的結果而言,銀行若要向客戶推廣辦理pep,以增加銀行的業績,那這個結果可以是一個被銀行拿來採納的有效應用,畢竟其Correctly Classified Instances(正確的分類案例)的正確率,比起我們前面在分析WaterTaste.csv與ExerciseHours.csv還高出非常多。銀行可以針對上述被決策樹的屬性條件歸類為「可能有辦理pep的客戶」,然後對其加強行銷pep的力道,如此一來,會比起去行銷被歸類為沒有辦理pep的客戶,還要有更高的成功率,也不需要用大海撈針、亂槍打鳥的方法去把全部的客戶逐一行銷一遍,這樣既浪費金錢、時間……等成本,亦無法以最有效率的方式去控制行銷成本。
2. 創意Dataset
假設銀行為了在銀行搶案發生的時候,讓警方辦案能夠迅速追蹤歹徒的下落,因此在銀行門口加裝了可以辨識身體外部特徵的儀器,此舉讓每位走進銀行的客戶,都會留下他們13種身體的資訊於銀行資料庫 : 「Weight(體重)」、「Height(身高)」、「Neck(脖圍)」、「Chest(胸圍)」、「Abdomen(腹圍)」、「Hip(臀圍)」、「Thigh(大腿圍)」「Knee(膝蓋圍)」、「Ankle(腳踝圍)」、「Biceps(二頭肌圍)」、「Forearm(前臂圍)」、「Wrist(手腕圍)」、「Fat_Percent(脂肪百分比)」。
(單位皆為公分,除了Weight的單位為公斤、Fat_Percent的單位為%)
因此,銀行就有了bank-data.csv裡面600位客戶的身體資料 :
創意Dataset 來源 → https://drive.google.com/file/d/1n2-_2EJ4IR9EbjhTgE4-mLxx5CaC5Obn/view?usp=sharing
有趣的問題就來了,我們想知道這些客戶在身材方面的特徵,是否也是讓他們辦理pep的重要依據之一?換句話說,有哪些身材特徵的人,會比較容易成為辦理pep的客戶?
下面一樣使用Decision Tree(決策樹)與REPTree(快速決策樹)這兩種方法來依序分析這筆創意Dataset :
① Decision Tree(決策樹)
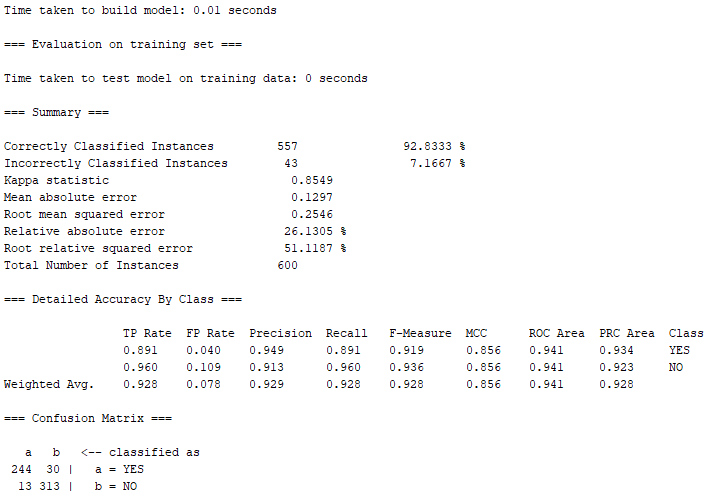
有557筆屬於Correctly Classified Instances(正確的分類案例),分類正確率達到約92.83%,相較單純bank-data.csv資料集的538筆成功案例多出了19筆。
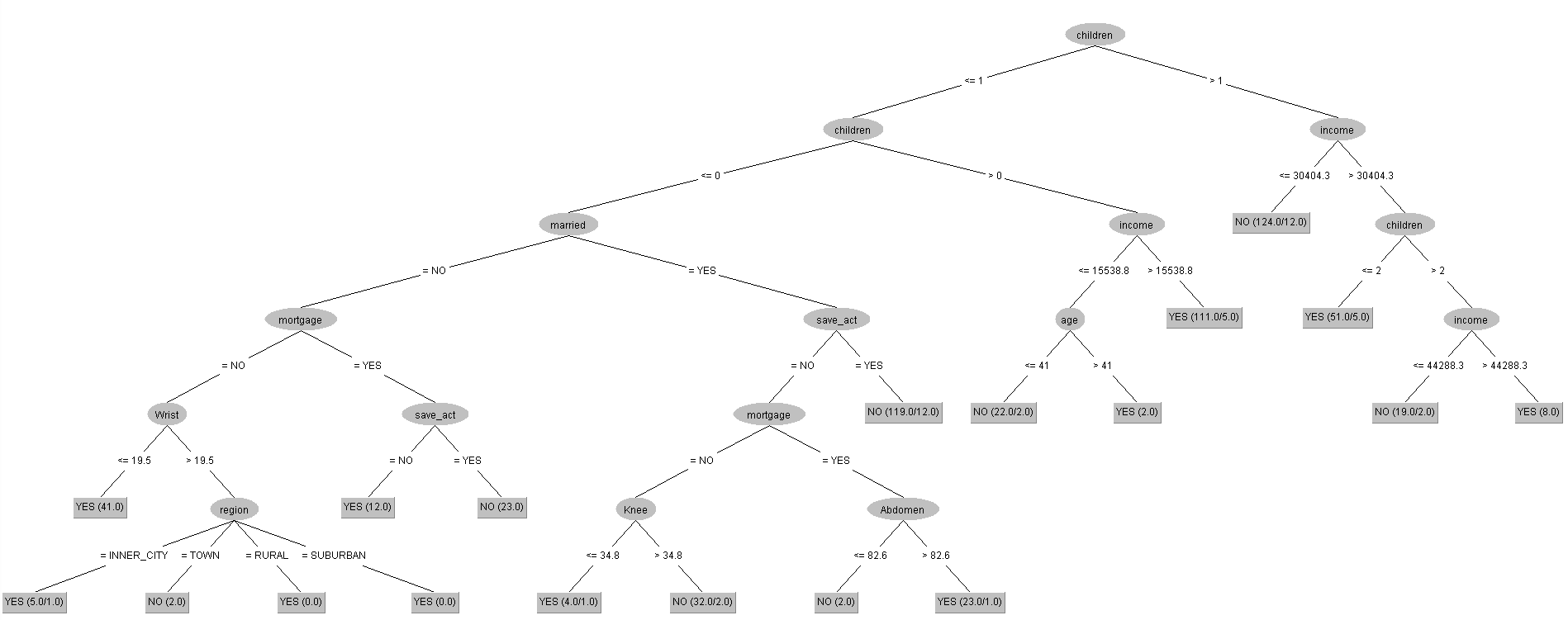
根據上述Decision Tree視覺化之後的結果,我們發現其與原先單純的bank-data.csv非常類似。
但11種符合會有高機率辦理pep的欄位屬性條件當中,當客戶是沒有小孩的情況下 : a. 有結婚、沒有儲蓄帳戶、且有抵押借款之紀錄、且腹圍大於82.6公分;b. 有結婚、沒有儲蓄帳戶、且沒有抵押借款之紀錄、且膝蓋圍小於等於34.8公分;c. 沒有結婚、且沒有抵押借款之紀錄、且手腕圍小於等於19.5公分;d. 沒有結婚、且沒有抵押借款之紀錄、且手腕圍大於19.5公分、且居住在除了都會區以外的地區,上述這四種情況為受到身特特徵的屬性所影響的結果。
因此,在加入與身材相關的特徵之後,「Neck(脖圍)」、「Abdomen(腹圍)」、與「Wrist(手腕圍)」,這三個屬性被Decision Tree視為較重要判斷是否會辦理pep的依據,其他身材特徵則被Decision Tree視為重要程度不高的欄位屬性。
② REPTree(快速決策樹)
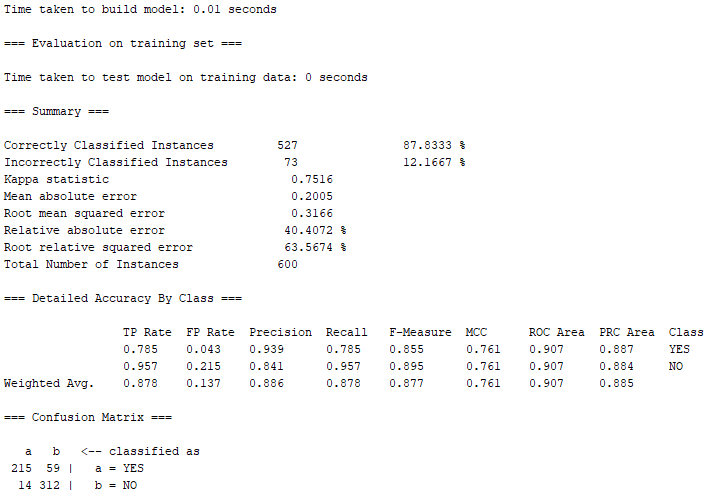
案例準確率如同用現有Data-set的結果一樣,Decision Tree的正確率表現較REPTree還高,而在這裡有527筆屬於Correctly Classified Instances(正確的分類案例),正確率約87.83%,依然略遜於上面Decision Tree跑出來的92.83%正確率,結果實屬不意外。
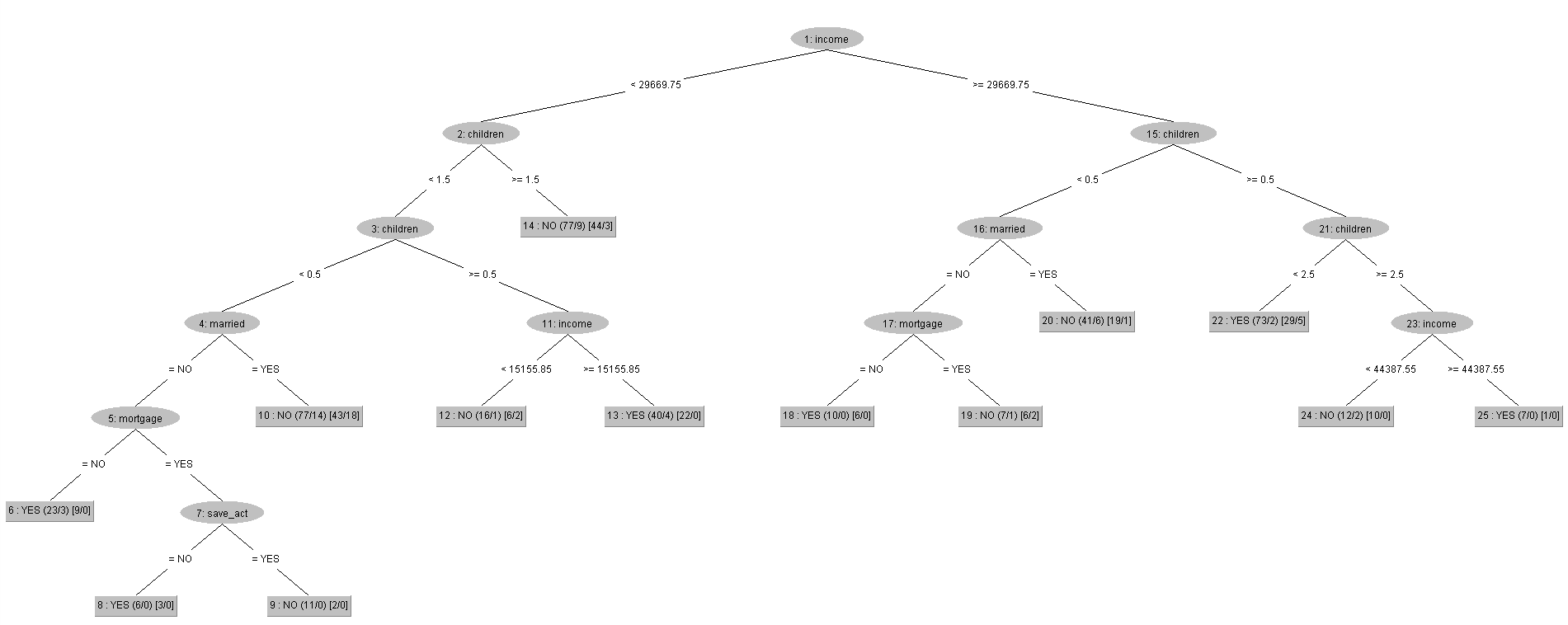
上面視覺化REPTree所跑出來的結果,可以發現其架構跟用現有Dataset去跑REPTree的結果幾乎一樣,唯一的差別就在於,當我們融入了身材特徵的欄位屬性之後,原本圖片當中的第10個tree節點是「Age(年齡)」,而且其下方的子節點還有「region(居住地區)」、「income(收入)」、「mortgage(是否有抵押借款的紀錄)」這三種屬性,如今第10個節點直接被REPTree判定為沒有辦理pep。
故在結合了每個客戶各自的身材特徵之後,REPTree認為當有客戶的條件是收入小於29669.75元、且沒有小孩、且有結婚的情況下,「Age(年齡)」、「region(居住地區)」、「income(收入)」、「mortgage(是否有抵押借款的紀錄)」這四個屬性與是否有辦理pep的相關性已降低,可以直接判定這類客戶有較高機率是屬於沒有辦理pep的那群。
針對① Decision Tree(決策樹)去分析創意Dataset的結果來說,銀行若要向客戶推廣辦理pep,那除了在前面有提到的,可以針對在現有Dataset被決策樹的屬性條件歸類為「可能有辦理pep的客戶」,對其加強行銷pep的力道之外,現在又能夠透過身材相關的欄位屬性去辨識。
只要客戶在剛走進銀行的時候,銀行專員就可以直接先以創意Dataset求得的結果 : 客戶腹圍是否大於82.6公分?膝蓋圍是否小於等於34.8公分?手腕圍是否小於等於19.5公分?手腕圍是否大於19.5公分?上述這些外貌特徵,去判斷該名客戶會去辦理pep的機率高不高。
等到之後再由銀行專員去比對其填寫的個人資料,如生育情況、婚姻、是否有儲蓄帳戶、是否有抵押借款之紀錄、居住地區……等與Decision Tree之分析相符的欄位屬性,就可以知道哪些客戶是在經過推銷之後容易答應辦理pep,相反亦然。
故當遇到身形條件與背景經歷都是被Decision Tree判定為有辦理pep之客戶的時候,銀行專員可以加強推銷與行銷的力度,即使起初被拒絕,但或許稍為盧一點,該名客戶就會答應辦理pep,進而增加銀行的業務量。
文章出自 — Bernard Huang
結語
這次的演算法分析有讓你感到腦袋炸裂嗎?如果想入門更多元的程式相關內容,可以到快樂學程式的Udemy逛逛,你絕對會在裡面奠定良好的程式基礎!

如果你的入門還在單打獨鬥,歡迎來到快樂學程式找到志同道合的夥伴,你的自學之路不孤單。







